FP-Growth* Algorithm (Frequent-Pattern Growth)

시작하기전에

바로 전 연관규칙분석 (Apriori Algorithm) 을 보지 못했다면, 그리고 Apriori를 잘 모른다면 잠깐이라도 보고 넘어오길 바란다. Apriori와 마찬가지로 수학적으로, 논문처럼 작성된 문서들은 널리고 널렸기에, 좀더 쉽고 간단하게 설명하고자한다.

어디까지나 알고리즘 이해를 중심으로 설명하려하기에, 알려진 논문이나 자료들과는 조금 다를지도 모른다. 애시당초 그런 논문들 처럼 설명할거였으면 그냥 링크나 올리고 말았을 것이다. ㅎㅎ

소개

FP-Growth는 FP-Tree라는 구조를 이용하여 Apriori를 효과적으로 구현한 것이라 나는 생각한다.

앞서 Apriori의 처리속도 문제를 해결할 수 있게끔, 자료구조를 기똥차게(?) 응용하여 만들어낸 트릭(?)이랄까?ㅋ (처음에 이거 이해하고 얼마나 놀라웠던지..ㅋㅋ)

FP-Tree의 구조는, Tree, Array, Linked-List를 합쳐놓은 구조이다. 자료구조에 밝은 사람이라면 누구나 이해가 쉬울 것이다. 

(얼핏 구성만 보면, 강남에서 프랑스인이 길을 묻는 것 같은 유체이탈을 경험하게 되지만, 세부적으로 하나하나 뜯어보면 사실 무쟈게 단순하다. ^^)

먼저, 구성을 보자.

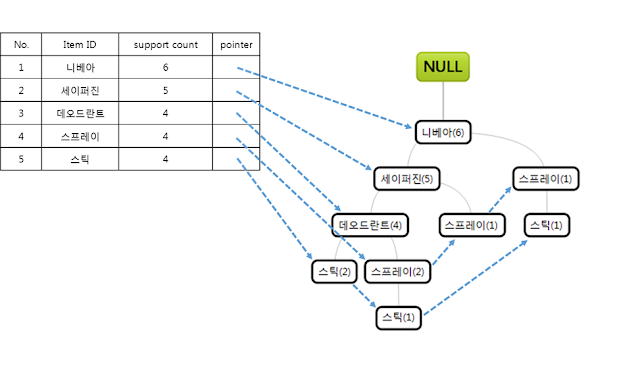
좌측의 Table은 Node-link(Pointer)를 가진 배열(frequent-item-header table)이다.
우측의 동그란원(Node)들과 실선 화살표는 트리(item-prefix sub-trees)이다. (Root-Node가 Null이라는 것을 주의하자.)
그리고 박스와 동그란원(Node)을 점선 화살표로 연결해 놨는데, 이것이 Linked-list 이다.

레시피

입력데이터 예시)
다음과 같은 상품정보가 있다고 생각해보자. (구성에서는 Item ID라며 I1~I5라는 코드로 되어있으나, 이해를 위해 실제 '인XX크 상품명'으로 예를 만들겠음)

1. 데오드란트, 니베아, 스틱, 세이퍼진
2. 니베아, 스프레이, 세이퍼진
3. 데오드란트, 니베아, 스틱, 세이퍼진
4. 데오드란트, 니베아, 스프레이, 세이퍼진
5. 데오드란트, 니베아, 스프레이, 스틱, 세이퍼진
6. 스프레이, 니베아, 스틱

각 item의 전체 노출 수를 구한 후, 빈도(support count)가 높은 순으로 정렬한다.

No.	Item ID	support count
1	니베아	6
2	세이퍼진	5
3	데오드란트	4
4	스프레이	4
5	스틱	4

이제 이 순서를 기준으로, 각각의 item을 정렬한다. (빈도가 높은 item이 앞에 놓인다.)

1. 니베아, 세이퍼진, 데오드란트, 스틱
2. 니베아, 세이퍼진, 스프레이
3. 니베아, 세이퍼진, 데오드란트, 스틱
4. 니베아, 세이퍼진, 데오드란트, 스프레이
5. 니베아, 세이퍼진, 데오드란트, 스프레이, 스틱
6. 니베아, 스프레이, 스틱

이 결과를 순서대로 Tree에 삽입한다. (괄호안의 숫자는 support count 이다.)

1. 첫 데이터 "니베아, 세이퍼진, 데오드란트, 스틱"이 차례로 입력된다. (키워드 옆의 (1)은, "1회씩 입력되었다"는 의미)
2. 두번째 데이터 "니베아, 세이퍼진, 스프레이"는 "니베아"와 "세이퍼진"이 각각 1회씩 추가되어 (2)로 변경되며, "스프레이"는 신규노드로 추가된다.
3. 세번째 데이터 "니베아, 세이퍼진, 데오드란트, 스틱"은 기존에 이미 만들어진 노드가 모두 있으므로 카운트만 달라진다.
4. 네번째 데이터 "니베아, 세이퍼진, 데오드란트, 스프레이"는 "니베아, 세이퍼진"이 이미 존재하므로 카운트만올리고 "데오드란트"의 하위에 "스프레이"가 없으므로 신규노드로 추가된다.
5. 다섯번째 데이터 "니베아, 세이퍼진, 데오드란트, 스프레이, 스틱"은 기존에 "니베아, 세이퍼진, 데오드란트"가 이미 존재하므로 카운트만 올리고 "스프레이"의 하위에 "스틱"이 없으므로 신규노드로 추가된다.
6. 여섯번째 데이터 "니베아, 스프레이, 스틱"은 "니베아" 카운트 증가 후 "스프레이, 스틱"이 없으므로 각각 차례로 신규 추가된다.

이제 아까 만들어놓은 배열(frequent-item-header table)과 지금 만들어진 Tree(item-prefix subtrees)를 아래와 같이 (같은 item끼리) Linked-list로 연결한다.

파란 점선 화살표의 진행을 유념하여 살펴보라.

각 노드의 괄호 안 숫자는 support count이며 횡으로 연결된 동일 노드들간 support count의 값을 합산하면 Header table의 support count값과 동일해진다.

자, 여기까지하면 일단 구조는 완성된 것이다.

매우 간단하고 쉽지않은가? ㅎㅎ (참고: https://fenix.tecnico.ulisboa.pt/downloadFile/3779571250096/licao_10.pdf )

그럼 이제부터, 연관키워드를 찾아내는 흐름을 설명하겠다.

빈발패턴을 찾아내기

먼저, 위 상품 데이터(니베아, 세이퍼진, 데오드란트 블라블라~)들 안에서 빈발패턴들을 찾아내보자.

위에서 만들어진 FP-Tree를 분해함으로서 아주 쉽게 얻을 수 있다. (분해는 항상 support count가 낮은 item부터 시작한다.)

그 전에 Apriori에서도 언급했다시피, 전체 데이터를 표본으로 삼는 것은 좋지않기 때문에 노이즈를 제거한다. 즉, Minimum support를 선언하지만, 패스하겠다.

제일 support count가 낮은 "스틱"을 기준으로 FP-Tree 內 해당 item을 찾는다.

1. "스틱"이 존재하지 않는 경로는 제거한다.
2. 그리고 support count를 업데이트하는데, 스틱의 support count를 고스란히 올려준다고 생각하면 된다.
3. 따라서 "스프레이"는 1이 되고, 데오드란트는 좌측 "스틱"의 2와 우측 "스틱"의 1이 합산된 3이 된다.
4. 같은 방법으로 부모노드의 support count를 업데이트 한다. 
5. 목표로 했던 item인 "스틱"을 제거하여, 최종트리를 완성한다.

솔직히 제거하던말던 별 차이는 없구만.. ㅎㅎ

support count가 낮은 "스프레이"를 배제하여보면, (니베아, 세이퍼진, 데오드란트, 스틱)(3), (니베아, 세이퍼진, 스틱)(3), (니베아, 데오드란트, 스틱)(3), (니베아, 스틱)(3)등의 부분집합이 만들어진다.

<(니베아, 세이퍼진, 데오드란트, 스틱) 에서 "스틱"에 맞닿은 "데오드란트"의 suport count의 값이 3이므로 (니베아, 세이퍼진, 데오드란트, 스틱)의 suport count 역시 3이 된다.>




같은 방법으로 "스프레이"를 기준으로 트리를 분해해보겠다.


"스프레이"을 기준하여, (니베아, 세이퍼진, 스프레이)(3), (니베아, 스프레이)(4), (세이퍼진, 스프레이)(3) 등의 부분집합이 만들어진다.

<(니베아, 세이퍼진, 스프레이) 에서 "스프레이"에 맞닿은 "세이퍼진"의 suport count의 값이 3이므로 (니베아, 세이퍼진, 스프레이)의 suport count 역시 3이 된다.>


"데오드란트", "세이퍼진", "니베아"도 차례로 분해하면, 각각 다음과 같은 모습이 된다.


이렇게 얻어진 패턴들이 빈발패턴이라 볼 수 있겠다. (support count를 기준으로 가중치를 조정할 수 있을 것이다.)

• "스틱"에서 얻을 수 있는 조합: (니베아, 세이퍼진, 데오드란트, 스틱)(3), (니베아, 세이퍼진, 스틱)(3), (니베아, 데오드란트, 스틱)(3), (니베아, 스틱)(4), (스틱)(4)
• "스프레이"에서 얻을 수 있는 조합: (니베아, 세이퍼진, 데오드란트, 스프레이)(3), (니베아, 세이퍼진, 스프레이)(3), (니베아, 스프레이)(4), (스프레이)(4)
• "데오드란트"에서 얻을 수 있는 조합: (니베아, 세이퍼진, 데오드란트)(4), (니베아, 데오드란트)(4), (세이퍼진, 데오드란트)(4), (데오드란트)(4)
• "세이퍼진"에서 얻을 수 있는 조합: (니베아, 세이퍼진)(5), (세이퍼진)(5)
• "니베아"에서 얻을 수 있는 조합: (니베아)(6)

결국 빨간색으로 표시한 것들을 중심으로 먼저 support count가 5인 Item-set (니베아, 세이퍼진)(5),

다음으로 support count가 4인 Item-set은, (니베아, 세이퍼진, 데오드란트)(4), (니베아, 데오드란트)(4), (세이퍼진, 데오드란트)(4), (니베아, 스프레이)(4), (니베아, 스틱)(4)

그 다음으로 support count가 3, 2, 1, …

등등의 순으로 빈발패턴이 만들어지게 된다.

FP-Growth vs Apriori

여기서 유념하여야 할 부분은 빈발패턴을 찾기위해 Apriori처럼 전체 트리를 탐색하지 않고,

Header table에서 해당 item을 찾아 Linked-list를 통해 차례로 접근하면 되기에 속도상 엄청난 이득을 가져올 수 있다는 점이다.

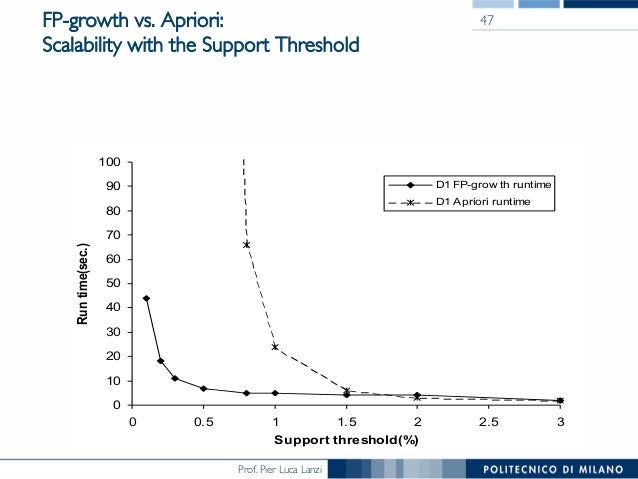
Apriori에서 말했듯, 워낙 비교횟수가 무지막지한 문제로 알고리즘의 퍼포먼스가 매우 안좋은데, FP-Tree에서는 그것을 효과적으로 개선했다.

※ Python package
https://pypi.org/project/pyfpgrowth/

마치며

경험상으로 미루어 볼때, 데이터의 수가 테라바이트급이로 올라가게 되면 (표본을 채취해서 분석에 활용한다해도 기가바이트급 이기에..), FP-Tree 역시 문제가 있더군요.

아시다시피 Linked-list의 퍼포먼스는 극악에 가깝지요. 매번 노드의 포인터를 찾아야할 때마다 부하가 엄청납니다. ( 속도가 나무늘보 움직이듯 하더라ㅜㅜ; )

이러한 FP-Growth의 단점들을 보완하여 많은 변형알고리즘이 존재하는데, FP-Growth Algorithm Variations 이곳에서 참고할 수 있습니다.


결국 같은 이유로 인해, 저 역시 다른 아이디어를 찾게 되었습니다. FP-Tree 그대로를 사용하지는 않고, 다른 형태로 변형/조작해서 사용하곤 했었습니다. ( 예를들어, Map-reduce )

FP-Growth를 이용하실 생각이라면 아마도 이러한 점을 유념하셔야 할 것입니다.

사실 라이브러리를 사용한다면, 세세하게 동작원리까지는 몰라도 될 수 있기에, 어디까지나 이해를 돕기위한 글이 되었으면 하는 바램입니다.